การเปลี่ยนการต่อสตาร์-เดลต้าและวงจรบริดจ์

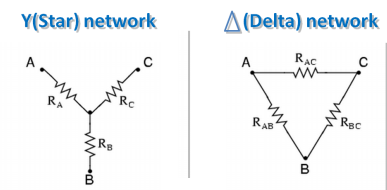
       ในวงจรไฟฟ้าที่ซับซ้อนบางครั้งไม่สามารถหาค่าความต้านทานรวมของวงจรได้ จากการใช้หลักการของวงจรขนานหรืออนุกรม การแปลงตัวต้านทานที่ต่อแบบสตาร์หรือเดลต้า จึงเป็นวิธีการแก้ปัญหาโจทย์วิธีหนึ่งที่ใช้ในกรณีที่มีการต่อวงจรตัวต้านทานแบบที่ไม่อยู่ในรูปแบบอนุกรมหรือขนานเมื่อแปลงรูปแบบการวางตัวต้านทานไปแล้วจะสามารถรวมค่าความต้านทานได้การต่อตัวต้านทานในที่นี้เป็นการเชื่อมต่อตัวต้านทานระหว่างจุดเชื่อมต่อ 3 จุด ในรูป 1 คือ จุด A B, C ซึ่งมี2 รูปแบบ คือ แบบสตาร์ (Star) หรือ วาย (Y) หรือ และอีกรูปแบบหนึ่งคือแบบเดลต้า (Delta) เป็นการเชื่อมโยงตัวต้านทานมี ลักษณะคล้ายรูปสามเหลี่ยม

รูปที่ 1 วงจรความต้านทานสตาร์-เดลต้า

การแปลงวงจรความต้านทานสตาร์-เดลต้า และ เดลต้า-สตาร์

       จากรูปที่ 1 สมการที่ใช้ในการแปลงวงจรตัวต้านทานจาก สตาร์(Y) เป็น เดลต้า(∆)หรือจากเดลต้าเป็นสตาร์ ทำได้โดยการใช้สมการการแปลงดังต่อไปนี้

การแปลงวงจรความต้านทานสตาร์-เดลต้า

รูปที่ 2 สูตรการแปลงความต้านทานสตาร์-เดลต้า

    สรุป การแปลงเดลต้า – สตาร์ “ค่าความต้านทานในเดลต้าจะมีค่าเท่ากับผลบวกของผลคูณของความต้านทานในสตาร์ทีละคู่หารด้วยความต้านทานในสตาร์ที่อยู่ตรงกันข้ามกับความต้านทานในเดลต้า ”

การแปลงวงจรความต้านทานเดลต้า – สตาร์

 

รูปที่ 3 สูตรการแปลงความต้านทานเดลต้า – สตาร์

    สรุป การแปลงเดลต้า – สตาร์ “ค่าความต้านทานในสตาร์จะมีค่าเท่ากับผลคูณของความต้านทานในเดลต้าที่ประกบอยู่ทั้งสองข้างในด้านเดียวกัน หารด้วยผลบวกของความต้านทานทุกตัวในเดลต้า ”

กรณีที่ค่าความต้านทานในวงจรสตาร์ หรือเดลต้า มีค่าเท่ากันทุกตัว

1.  ถ้า RA = RB =RC = RY 
   
2.  ถ้า RAB = RBC =RCA = R∆

เรียกว่า วงจรสตาร์สมดุลและเดลต้าสมดุล จะได้ความสัมพันธ์ระหว่างวงจรสตาร์และเดลต้า ดังต่อไปนี้คือ ความต้านทานสตาร์จะเท่ากับความต้ารทานเดลต้าหารด้วยสาม

ตัวอย่างที่ 1 วงจรบริดจ์ดังรูปที่ 4 จงหาค่ากระแสไฟฟ้ารวมที่แหล่งจ่ายไฟฟ้าจ่ายออกมา

รูปที่ 4 ตัวอย่างวงจรบริดจ์

              วิธีทำ  จากวงจรนี้จะเห็นว่าไม่สามารถหาค่าความต้านทานรวม RT ของวงจรที่เกิดจากการ รวมกันแบบขนานหรืออนุกรม จากตัวต้านทาน R1 – R5  ได้จึงต้องนำวิธีการแปลงสตาร์ - เดลต้ามาใช้ให้พิจารณาจากรูปต่อไปนี้ทีละขั้นตอน

 วงจรบริดจ์ (bridge circuit)

        วงจรบริดจ์ (bridge circuit) เป็นเครื่องมือที่ใช้วัดค่าความต้านทานในวงจรไฟฟ้ากระแสตรงที่มีความถูกต้องสูงซึ่งในปัจจุบันนิมยมใช้แบบวิทสโตนบริดจ์ (wheatstone bridge) โดยวงจรวิทสโตนบริดจ์นี้ประกอบไปด้วย

1.  ตัวต้านทานที่ต่อขนานกัน 2 สาขา แต่ละสาขาประกอบด้วยตัวต้านทาน 2 ตัวต่ออนุกรมกัน
2.  แหล่งจ่ายไฟกระแสตรง(E) ต่อขนานกับวงจร
3.  กัลป์วานอมิเตอร์ต่อเข้ากับขั้วที่ขนานกัน คอยตรวจจับกระแสไฟฟ้า

 1.1 วงจรบริดจ์สมดุล (balanced bridge circuit) 

       วงจรบริดจ์ที่อยู่ในสภาพสมดุลไม่มีกระแสไหลผ่านกัลป์วานอมิเตอร์หรือเข็มของกัลป์วานอมิเตอร์ชี้ที่เลขศูนย์

 

รูปที่ 5 วงจรบริดจ์

 จากรูปที่ 5 ถ้าต้องการวัดค่าความต้านทานของ R4 จะต้องปรับอัตราส่วนของ R2/R1 และค่าความต้านทาน ของ R3 จนกระทั่งกระแสที่ไหลผ่านกัลป์วานอมิเตอร์จะมีค่าเป็นศูนย์ หรือวงจรบริดจ์สมดุลแล้วนั่นเอง

เมื่อไม่มีกระแสไหลผ่านกัลป์วานอมิเตอร์ แสดงว่า 𝐼1 = 𝐼3 และ 𝐼2 = 𝐼4

แทนค่า 𝐼3 ด้วย 𝐼1 และ 𝐼4 ด้วย 𝐼2 ลงในสมการที่ 1 จะได้

 หารสมการที่ 2 ด้วยสมการที่ 3 จะได้

 

 

 ตัวอย่างที่ 2 จงหาค่าความต้านทาน Rx จากวงจรบริดจ์ในสภาวะสมดุลดังรูปกำหนดให้R1 = 8Ω, R2 = 18Ω, R3 = 32Ω และ E = 24V

 วิธีทำ จาก

ตัวอย่างที่ 3 จากรูปจงหาค่าความต้านทานในขณะที่เข็มของกัลป์วานอมิเตอร์ชี้ที่เลขศูนย์ กำหนดให้ R1 = 15Ω, R3 = 36Ω, R4 = 75Ω และ E = 10V

 

 วิธีทำ จาก

 

1.2 วงจรบริดจ์ไม่สมดุล (unbalanced bridge circuit) 

       ในขณะที่บริดจ์มีสภาพไม่สมดุลจะมีกระแสไฟฟ้าไหลผ่านกัลป์วานอมิเตอร์ ทำให้เข็มของกัลป์วานอมิเตอร์เบี่ยงเบนไปจากศูนย์

 

รูปที่ 4.2 วงจรบริดจ์ไม่สมดุล

 จากรูป ในสภาวะบริดจ์ไม่สมดุลจะได้

ตัวอย่างที่ 4 จากรูปวงจรบริดจ์สมดุลหรือไม่ (จงพิสูจน์) ถ้าไม่สมดุลจะต้องใช้ค่า Rx เท่าใดวงจรบริดจ์นี้จึงจะสมดุลกำหนดให้R1 = 20Ω, R2 = 100Ω, R3 = 40Ω, Rx = 40Ω

 

 วิธีทำ จากรูป

 แทนค่า

บริดจ์ไม่สมดุล

ดังนั้น ถ้าต้องการให้วงจรบริดจ์สมดุลจะต้องใช้ค่า Rx ดังนี้

ตัวอย่างที่ 5 จากรูป ถ้าวงจรบริดจ์สมดุล โดยที่ Rv = 15kΩ และอัตราส่วน R2/R4 = 0.02 จงหา Rx

  วิธีทำ จากรูป